Системы счисления — это способ записи чисел с помощью определённых символов. Главная идея: у каждой системы счисления есть своё основание, которое определяет, сколько разных цифр можно использовать. В каждой системе счисления значение числа зависит от: цифры, его позиции в числе (разряд).
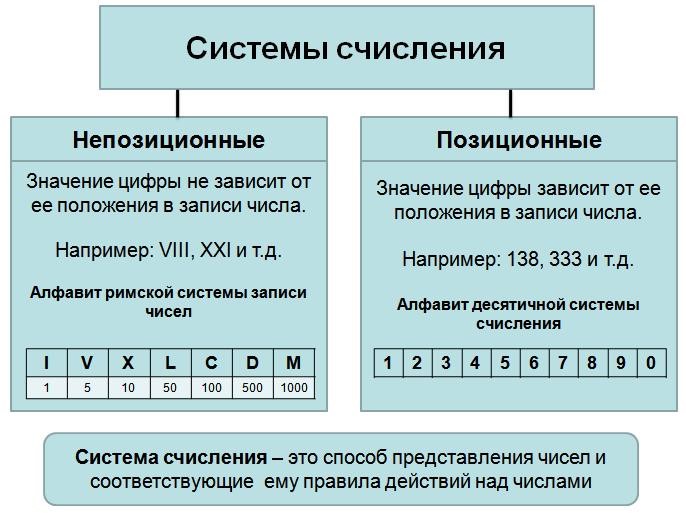
Почему это важно?
- В информатике (например, двоичная система — это язык компьютеров).
- В программировании (шестнадцатеричная система для цветов и адресов памяти).
- В технике (восьмеричная система использовалась в ранних компьютерах).
| Двоичная система (основание 2) Используются только две цифры: 0 и 1. Пример: 1012- это двоичное число. |
| Восьмеричная система (основание 8): Используются восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Пример: 278 -это восьмеричное число. |
| Десятичная система (основание 10): Мы используем её каждый день. Используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Пример: 12510 — это привычное нам число. |
| Шестнадцатеричная система (основание 16): Используются цифры: 0–9 и буквы A, B, C, D, E, F. Буквы обозначают числа: A=10, B=11, C=12, D=13, E=14, F=15. Пример: A316 — это шестнадцатеричное число. |
ТАБЛИЦА СООТВЕТСТВИЯ ЧИСЕЛ В РАЗНЫХ СИСТЕМАХ СЧИСЛЕНИЯ
| Десятичная (10) | Двоичная (2) | Восьмеричная (8) | Шестнадцатеричная (16) |
| 0 | 0 | 0 | 0 |
| 1 | 01 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
| 17 | 10001 | 21 | 11 |
| 18 | 10010 | 22 | 12 |
| 19 | 10011 | 23 | 13 |
| 20 | 10100 | 24 | 14 |
*Перед тестом обязательно распиши на листке вот такую таблицу
ПЕРЕВОД ЧИСЛА ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ В ДРУГИЕ (2, 8, 16)
ДЕЛАЕТСЯ С ПОМОЩЬЮ МЕТОДА ДЕЛЕНИЯ С ОСТАТКОМ
Перевод десятичного числа в двоичную систему (основание 2)
Пример: Переведём число 45 из десятичной системы в двоичную (2), восьмеричную (8), и шестнадцатеричную (16).
Шаги:
- Делим число на 2, записываем остатки.
- Повторяем деление, пока результат не станет 0.
- Читаем остатки снизу-вверх.
| Вариант 1 | Вариант 2 |
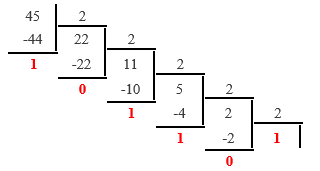 |  |
Остатки (снизу-вверх): 101101.
Ответ: 4510 = 1011012
Перевод десятичного числа в восьмеричную систему (основание 8)
Шаги:
- Делим число на 8. Записываем целую часть и остаток.
- Повторяем деление для целой части, пока результат не станет 0.
- Читаем остатки снизу-вверх.
| Вариант 1 | Вариант 2 |
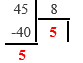 |  |
Остатки (снизу-вверх): 55
Ответ: 4510 = 558
Перевод десятичного числа в шестнадцатеричную систему (основание 16)
Шаги:
- Делим число на 16. Записываем целую часть и остаток.
- Повторяем деление для целой части, пока результат не станет 0.
- Читаем остатки снизу-вверх.
| Вариант 1 | Вариант 2 |
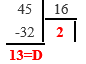 |  |
Остатки (снизу-вверх): 2D
Ответ: 4510 = 2D16
ПЕРЕВОД ЧИСЛА ИЗ ДВОИЧНОЙ СИСТЕМЫ В ДРУГИЕ (10, 8, 16)
Перевод числа из двоичной в десятичную (основание 10)
Принцип: Каждая цифра двоичного числа умножается на 2n, где n — её позиция справа налево (начиная с 0). Затем всё складывается.
Пример: переведём 10112 в десятичную систему.
Записываем степени 2 под каждой цифрой (справа налево🡐): (1×23) + (0×22) + (1×21) + (1×20)
Считаем: (1×8) + (0×4) + (1×2) + (1×1) = 8+0+2+1=11
(8 мы получили потому, что 23, получается мы умножаем 2×2×2 и т.д.)
Ответ: 10112=1110
Перевод числа из двоичной в восьмеричную (основание 8)
Принцип: Объединяем цифры в группы по 3 бита справа налево.Каждую группу переводим в восьмеричную цифру
Пример: переведём 1010112 в восьмеричную систему.
Разбиваем число на группы по 3 бита справа налево:101 011
Переводим каждую группу: 1012=5
(почему 101=5, ответ прост в двоичной системе счисления 101 при переводе в восьмеричную систему получается 5)
0112=38
Ответ: 1010112=538
Перевод числа из двоичной в шестнадцатеричную (основание 16)
Принцип: Объединяем цифры в группы по 4 бита справа налево. Каждую группу переводим в шестнадцатеричную цифру.
Пример: переведём 110101112 в шестнадцатеричную систему.
Разбиваем число на группы по 4 бита: 1101 0111 Переводим каждую группу:
Переводим каждую группу:
11012=D16
01112=716
Ответ: 110101112=D716
‼️────Итоговые правила перевода:────‼️
- В десятичную: Умножаем цифры на степени 2 и складываем.
- В восьмеричную: Разбиваем на группы по 3 бита.
- В шестнадцатеричную: Разбиваем на группы по 4 бита.
ПЕРЕВОД ЧИСЛА ИЗ ВОСЬМИРИЧНОЙ СИСТЕМЫ В ДРУГИЕ (10, 2, 16)
Перевод числа из восьмеричной в десятичную (основание 10)
Принцип: Каждая цифра восьмеричного числа заменяется на 3 двоичных бита.
Пример: переведём 2758 в двоичную систему.
Берём каждую цифру и заменяем на 3-битное двоичное число:
28=0102
78=1112
58=1012
Объединяем:
010 111 101
Ответ: 2758=0101111012
(Можно убрать незначащие нули слева: 10111101)
Перевод числа из восьмеричной в шестнадцатеричную (основание 16)
Принцип: Сначала переводим число в двоичную систему (см. выше). Делим двоичное число на группы по 4 бита. Каждую группу переводим в шестнадцатеричную цифру.
Пример: переведём 2758 в шестнадцатеричную систему.
Мы уже знаем, что:
2758=101111012
Разбиваем 10111101 на группы по 4 бита справа налево:
1011 1101
Переводим в шестнадцатеричные цифры:
10112=B16
11012=D16
Ответ: 2758=BD16
‼️────Итоговые правила перевода:────‼️
- В десятичную → Умножаем цифры на степени 8 и складываем.
- В двоичную → Каждую цифру заменяем на 3 бита.
- В шестнадцатеричную → Переводим в двоичную, затем группируем по 4 бита.
ПЕРЕВОД ЧИСЛА ИЗ ШЕСТНАДЦАТЕРИЧНОЙ СИСТЕМЫ В ДРУГИЕ СИСТЕМЫ (10, 2, 8)
Перевод из шестнадцатеричной в десятичную (основание 10)
Принцип: Каждая цифра шестнадцатеричного числа умножается на 16 в степени её позиции (считаем справа налево, начиная с нуля), а затем всё складываем.
Пример: переведём 2F316 в десятичную систему.
Записываем степени 16 под каждой цифрой:
(2×162) + (F×161) + (3×160)
Подставляем значения:
2×162=2×256=512
F=15, поэтому 15×161=15×16=240
3×160=3×1=3
Складываем:
512+240+3=755
Ответ: 2F316=75510
Перевод из шестнадцатеричной в двоичную (основание 2)
Принцип: Каждая цифра шестнадцатеричного числа заменяется на 4 двоичных бита.
Пример: переведём 2F316 в двоичную систему.
Берём каждую цифру и заменяем её на 4-битное двоичное представление:
216=00102
F16=11112
316=00112
Объединяем:
0010 1111 0011
Ответ: 2F316=0010 1111 00112
(Можно убрать незначащие нули слева: 1011110011)
Перевод из шестнадцатеричной в восьмеричную (основание 8)
Принцип: Сначала переводим число в двоичную систему (см. выше). Делим двоичное число на группы по 3 бита (справа налево). Каждую группу переводим в восьмеричную цифру.
Пример: переведём 2F316 в восьмеричную систему.
Мы уже знаем, что:
2F316 = 10111100112
Разбиваем 1011110011 на группы по 3 бита справа налево:
1 011 110 011
(Добавляем ноль слева, чтобы получить полные группы):
001 011 110 011
Переводим в восьмеричные цифры:
0012=18
0112=38
1102=68
0112=38
Ответ: 2F316=13638
‼️────Итоговые правила перевода:────‼️
- В десятичную → Умножаем цифры на степени 16 и складываем.
- В двоичную → Каждую цифру заменяем на 4 бита.
- В восьмеричную → Переводим в двоичную, затем группируем по 3 бита.
🤫🤫🤫Секрет перевода чисел в разные системы счисления🤫🤫🤫
💡 Запомни главный принцип💡
Любое число можно сначала перевести в десятичную систему (10), а потом в любую другую (2, 8, 16).
Почему?
Потому что десятичная система нам привычнее, и так проще считать! Если ты сдаёшь ЕНТ, этот метод поможет тебе быстро справляться с задачами без ошибок.
| Система | Цифры, которые используются | Принцип перевода в другие |
| Двоичная (2) | 0, 1 | Группируем по 3 для восьмеричной, по 4 для шестнадцатеричной |
| Восьмеричная (8) | 0, 1, 2, 3, 4, 5, 6, 7 | Сначала в двоичную (3 бита), затем в десятичную |
| Десятичная (10) | 0–9 | Нам привычная, используется для промежуточного перевода |
| Шестнадцатеричная (16) | 0–9, A(10), B(11), C(12), D(13), E(14), F(15) | Сначала в двоичную (4 бита), затем в десятичную |